Ethical issues aside, should you be honest when asked how certain you are about some belief? Of course, it depends. In this blog post, you’ll learn on what.
- Different ways of evaluating probabilistic predictions come with dramatically different degrees of “optimal honesty”.
- Perhaps surprisingly, the linear function that assigns +1 to true and fully confident statements, 0 to admitted ignorance and -1 to wrong but fully confident statements incentivizes exaggerated, dishonest boldness. If you rate forecasts that way, you’ll be surrounded by self-important fools and suffer from badly calibrated machine forecasts.
- If you want people (or machines) to give their truly unbiased and honest assessment, your scoring function should penalize confident but wrong convictions more strongly than it rewards confident correct ones.
A probabilistic quiz game
David Spiegelhalter’s new (as of 2025) fantastic book, “The Art of Uncertainty” – a must-read for everyone who deals with probabilities and their communication – features a short section on scoring rules. Spiegelhalter walks the reader through the quadratic scoring rule, and briefly mentions that a linear scoring rule will lead to dishonest behavior. I elaborate on that interesting point in this blog post.
Let’s set the stage: Just like in so many other scenarios and paradoxes, you find yourself in a TV show (yes, what an old-fashioned way to start). You have the opportunity to answer questions on common knowledge and win some cash. You are asked yes/no-questions that are expressed in a binary fashion, such as: Is the area of France larger than the area of Spain? Was Marie Curie born earlier than Albert Einstein? Is Montreal’s population larger than Kyoto’s?
Depending on your background, these questions might be obvious for you, or they might be difficult. In any case, you will have a subjective “best guess” in mind, and some degree of certainty. For example, I feel comfortable answering the first, slightly less for the second, and I already forgot the answer to the third, even though I looked it up to build the example. You might experience a similar level of confidence, or a very different one. Degrees of certainty are, of course, subjective.
The twist of the quiz: You are not supposed to give a binary yes/no-answer as in a multiple-choice test, but to honestly communicate your degree of conviction, that is, to produce the probability that you personally assign to the true answer being “yes”. The number 0 then means “definitely not”, 1 expresses “definitely yes”, and 0.5 reflects the degree of uncertainty corresponding to the toss of a fair coin — you then have absolutely no idea. Let’s call P(A) your true subjective conviction that statement A is true. That probability can take any value between 0 and 1, whereas A is bound to be either 0 or 1. You can then communicate that number, but you don’t have to, so we’ll call Q(A) the probability that you eventually express in that quiz.
In general, not every probabilistic expression Q is met with the same excitement, because humans generally dislike uncertainty. We are much happier with the expert that gives us “99.99%” or “0.01%” probabilities for something to be or not to be the case, and we favor them considerably over the experts producing “25%” and “75%” maybe-ish assessments. From a rational perspective, more informative probabilities (“sharp predictions”, close to 0 or close to 1) are favorable over uninformative ones (“unsharp predictions”, close to 0.5). However, a modest but truthful prediction is still worth more than a bold but unreliable one that would make you go all-in. We should therefore ensure that people do not lie about their degree of conviction, so that really 99% of the “99%-sure” predictions are actually true, 12% or the “12%-sure”, and so on. How can the quiz master ensure that?
The Linear Scoring Rule
The most straightforward way that one might come up with to judge probabilistic statements is to use a linear scoring rule: In the best case, you are very confident and right, which means Q(A)=P(A)=1 and A is true, or Q(A)=P(A)=0 and A is false. We then add the score +1=r(Q=1, A=1)=r(Q=0, A=0) to the balance. In the worst case, you were very sure of yourself, but wrong; that is, Q(A)=P(A)=1 while A is false, or Q(A)=P(A)=0 while A is true. In that unfortunate case, we subtract –1=r(Q=1, A=0)=r(Q=0, A=1) from the score. Between these extreme cases, we draw a straight line. When you express maximal uncertainty via Q(A)=0.5, we have 0=r(Q=0.5, A=1)=r(Q=0.5, A=0), and neither add nor subtract anything.
The functional form of this linear reward function is not particularly spectacular, but its visualization will come handy in the following:
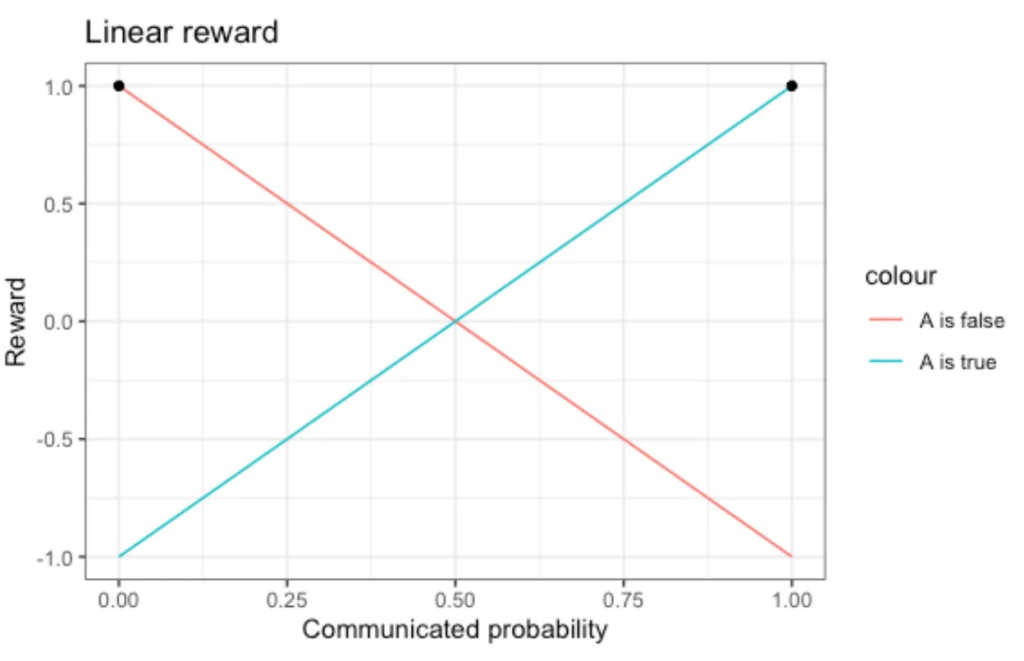
No surprise here: If A is true, the best thing you could have done is to communicate “Q=1”, if A is false, the best strategy would have been to produce “Q=0”. That’s what is visualized by the black dots: They point to the largest value that the reward function can attain for the particular value of the truth. That’s a good start.
But you typically do not know with absolute certainty whether the answer is “yes, A is true” or “no, A is false”, you only have a subjective gut feeling. So what should you do? Should you just be honest and communicate your true belief, e.g. P=0.7 or P=0.1?
Let’s set ethics aside, and consider the reward that we want to maximize. It then turns out that you should not be honest. When evaluated via the linear scoring rule, you should lie, and communicate Q(A)=0 when P(A)<0.5 and Q(A)=1 when P(A)>0.5.
To see this surprising result, let’s compute the expectation value of the reward function, assuming that your belief is, on average, correct (cognitive psychology teaches us that this is an unrealistically optimistic assumption in the first place, we’ll come back to that below). That is, we assume that in about 70% of the cases when you say P=0.7, the true answer is “yes, A is true”, in about 75% of the cases when you say P=0.25, the true answer is “no, A is false”. The expected reward R(P, Q) is then a function of both the honest subjective probability P and of the communicated probability Q, namely the weighted sum of the reward r(Q, A=1) and r(Q, A=0):
R(P, Q) = P * r(Q, A=1) + (1-P) * r(Q, A=0)
Here come the resulting R(P,Q) for four different values of the honest subjective probability P:
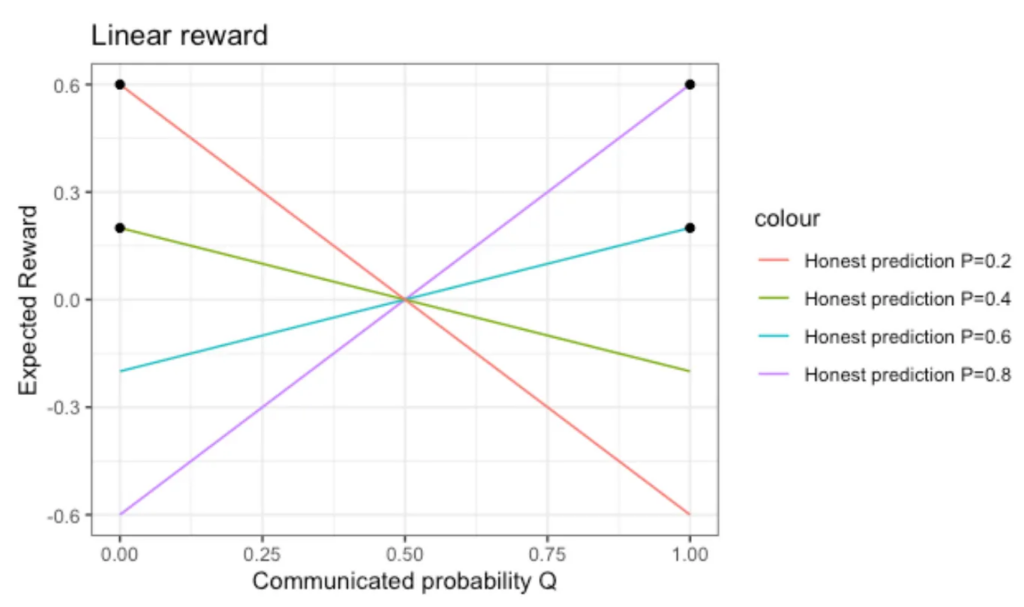
The maximally attainable reward on the long term is not always 1 anymore, but it’s bounded by 2|P-0.5| — ignorance comes at a cost. Clearly, the best strategy is to confidently communicate Q=1 as long as P>0.5, and to communicate an equally confident Q=0 when P<0.5 — see where the black dots lie in the figure.
Under a linear scoring rule, when it is more likely than not that the event occurs — pretend you are absolutely certain that it will occur. When it’s marginally more likely that it does not occur — be bold and proclaim “that can never happen”. You will be wrong sometimes, but, on average, it’s more profitable to be bold than to be honest.
Even worse: What happens when you have absolutely no clue, no idea about the outcome, and your subjective belief is P=0.5? Then you can play safe and communicate that, or you can take the chance and communicate Q=1 or Q=0 — the expectation value is the same.
If find this a disturbing result: A linear reward function makes people go all-in! There is no way as forecast consumer to distinguish a slight tendency of 51% from a “quite likely” conviction of 95% or from an almost-certain 99.9999999%. In that quiz, the smart players will always go all-in.
Worse, many situations in life reward unsupported confidence more than thoughtful and careful assessments. Cautiously said, not many people are being heavily sanctioned for making clearly exaggerated claims…
A quiz show is one thing, but, obviously, it’s quite a problem when people (or machines…) are pushed to not communicate their true degree of conviction when it comes to estimating the risk of serious and dramatic events such as earthquakes, war and catastrophes.
How can we make them to be honest (in the case of people) or calibrated (in the case of machines)?
Punishing confident wrongness: The Quadratic Scoring Rule
If the probability for something to happen is estimated to be P=55% by some expert, I want that expert to communicate Q=55%, and not Q=100%. For probabilities to have any value for our decisions, they should reflect the true level of conviction, and not an opportunistically optimized value.
This reasonable ask has been formalized by statisticians by proper scoring rules: A proper scoring rule is one that incentivizes the forecaster to communicate their true degree of conviction, it is maximized when the communicated probabilities are calibrated, i.e. when predicted events are realized with the predicted frequency. At first, the question might arise whether such a scoring rule can exist at all. Thankfully, it can!
One proper scoring rule is the quadratic scoring rule, also known as the Brier score. For extreme communicated probabilities (Q=1, Q=0), the values are the very same as for the linear scoring rule, but we don’t draw straight line between these, but a parabola. By doing that, we reward honest ignorance: +0.5 is awarded for a communicated probability of Q=0.5.

This reward function is asymmetric: When you increase your confidence from Q=0.95 to Q=0.98 (and A is true), the reward function only increases marginally. On the other hand, when A is false, that same increase of confidence leaning towards the wrong outcome is pushing down the reward considerably. Clearly, the quadratic reward thereby nudges one to be more cautious than the linear reward. But will it suffice to make people honest?
To see that, let’s compute the expectation value of the quadratic reward as a function of both the true honest probability P and the communicated one Q, just like we did in the linear case:
R(P, Q) = P * r(Q, A=1) + (1-P) * r(Q, A=0)
The resulting expected reward, for different values of the honest probability P, is shown in the next figure:
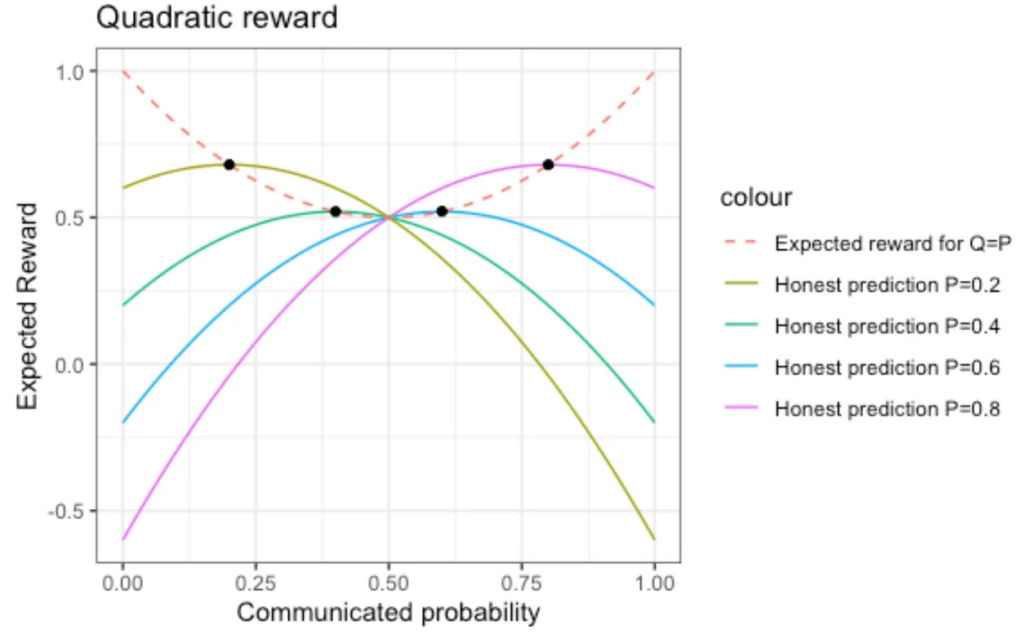
Now, the maxima of the curves lie exactly at the point for which Q=P, which makes the correct strategy communicating honestly one’s own probability P. Both exaggerated confidence and excessive caution are penalized. Of course, by knowing more in the first place, you’ll be able to make sharper and more confident statements (more predictions Q=P that are either close to 1 or close to 0). But honest ignorance is now rewarded with +0.5. Better be safe than sorry.
What do we learn from that? The reward that is maximized by honestly communicated probabilities sanctions “surprises” (Q<0.5 and the event is actually true, or Q>0.5 and the event is actually false) quite strongly. You lose more when you are wrong with your tendency (Q>0.5 or Q<0.5) than you would win when you are correct. At the same time, not knowing and being honest about it is rewarded a non-negligible value.
Logarithmic reward
The quadratic reward function is not the only one that rewards honesty (there are infinitely many proper scoring rules): The logarithmic reward penalizes being confidently wrong (P=0, but truth is “yes, A is true”; P=1, yet truth is “no, A is false”) with an unassailable -infinity: The score is simply the logarithm of the probability that had been predicted for the event that eventually occurred — the plot is cut off on the y-axis for that reason:
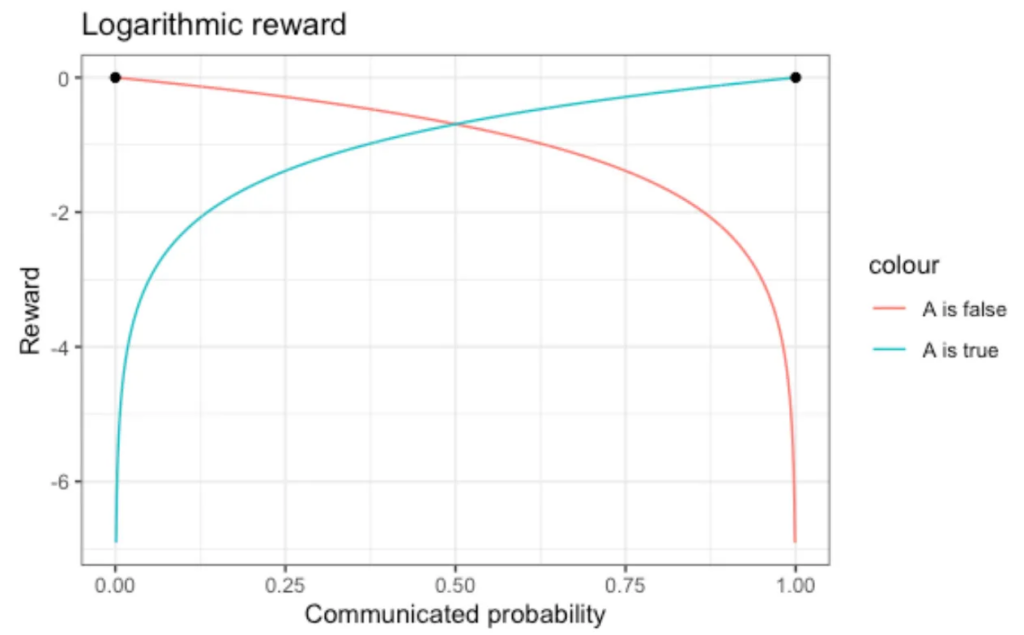
The logarithmic reward breaks the symmetry between “having communicated a slightly too-high” and “having expressed a slightly too-low” probability: Towards uninformative Q=0.5, the penalty is weaker than towards informative Q=0 or Q=1, which we see in the expectation values:

The logarithmic scoring rule heavily penalizes the assignment of a probability of 0 to something that then very surprisingly happened: Somebody who has to admit “I really though it was absolutely impossible” after the fact that they assigned Q=0 won’t be invited to provide predictions ever again…
Incentivizing sandbagging: The Cubic Scoring Rule
Scoring rules can push forecasters to be over-confident (see the linear scoring rule), they can be proper (see the quadratic and logarithmic scoring rules), but they can also punish “being boldly wrong” so thoroughly that forecasters would rather pretend they don’t know really even if they do. A cubic scoring rule would lead to such excessive caution:

The expectation values of the reward now make people rather communicate values that are less informative (closer to 0.5) than their true convictions: Instead of an honest Q=P=0.2, the optimum is at Q=0.333, instead of honest Q=P=0.4, the optimum is Q=0.4495.

In other words, to be provided honest judgements, don’t exaggerate the punishment of strong but eventually wrong convictions either — otherwise you’ll be surrounded by indecisive and hesitant cowards…
Honest and communicated probabilities
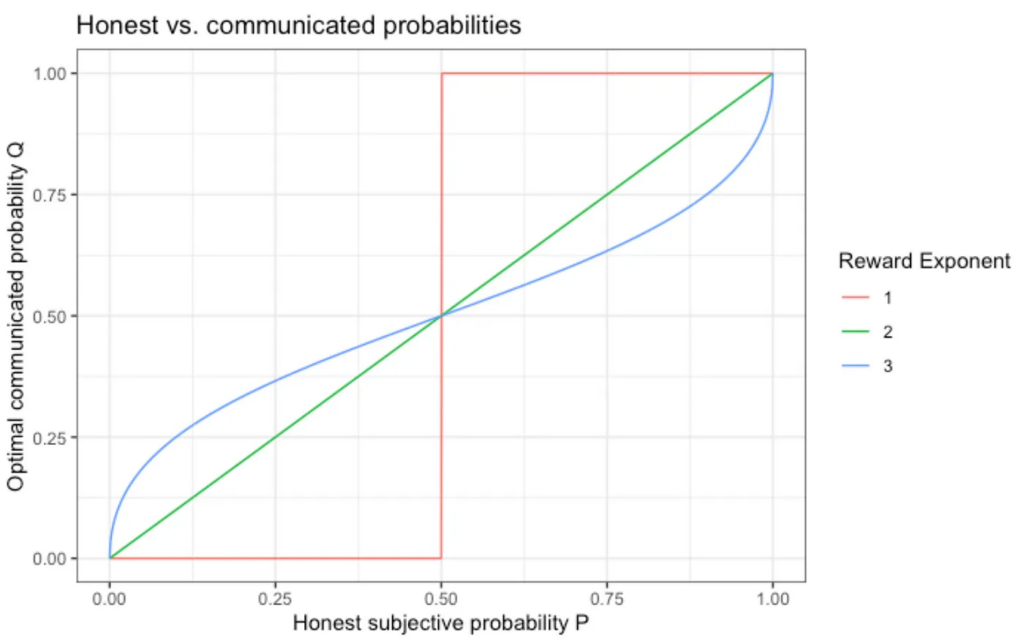
The following plot recapitulates the argument by showing the optimal communicated probability Q as a function of the true belief P. For a linear reward (Exponent 1), you will either communicate Q=0 or Q=1, and not disclose any information about your true degree of conviction. The quadratic reward (Exponent 2) makes you be honest (Q=P), while the cubic reward (Exponent 3) lets you set overly cautious Q values.
In reality, our choices are often binary, and, depending on the “false positive” and “false negative” cost and the “true positive” and “true negative” reward, we will set the threshold on our subjective probability to take or not take a certain action to different values. It is not at all irrational to plan thoroughly for a probability P=0.01=1% catastrophe.
If probabilities are subjective, how can they be “wrong”?
Scoring rules have two main applications: On a technical level, when training a probabilistic statistical or machine learning model on data, optimizing a proper scoring rule will yield calibrated and as-sharp-as-possible probabilistic forecasts. In a more informal setting, when several experts estimate the probability for something (typically dramatic) to happen, one wants to make sure that the experts are honest and don’t try to overplay or downplay their subjective uncertainty (beware of group dynamics!). Super-forecasters indeed use quadratic scoring rules to help reflect on their degree of confidence and to train themselves to become more calibrated.
Back to our initial quiz game. Before answering, you should definitely ask how you are evaluated. The evaluation procedure does matter, even if you are told it does not. Similarly, when you are given a multiple-choice-test, be sure to understand whether it might be worthwhile to check a box even if you are only very marginally certain about its correctness.
But how can a quiz involving subjective probabilities be evaluated at all in an objective fashion? According to Bruno De Finetti, “probability does not exist”, so how can we then judge the probabilities that people express? We don’t judge people’s taste either! David Spiegelhalter emphasizes in “The Art of Uncertainty” that uncertainty is not “a property of the world, but of our relationship with the world”.
However, subjective does not mean unfalsifiable.
I might be 99% sure that France is larger than Spain, 75% sure that Marie Curie was born before Albert Einstein, and 55% sure that Montreal is larger than Kyoto. The numbers that you assign to these statements will probably (pun intended) be different. Your relationship to the world is a different one than mine. That’s OK.
We can be both right in the sense that we express calibrated probabilities, even if we assign different probabilities to the same events.
A more commonplace setting: When I enter a supermarket, I can assign quite informative (quite high or quite low) probabilities to me buying certain products — I typically know well what I intend to shop. The data scientist working at the supermarket does not know my personal shopping list, even after having collected considerable personal data. The probability that they assign to me buying a bottle of orange juice will be quite different from the one that I assign to me doing that — both probabilities can be “correct” in the sense that they are calibrated on the long term.
Subjectivity does not mean arbitrariness: We can aggregate predictions and outcomes, and evaluate to which extent the predictions are calibrated. Scoring rules help us precisely with that task, because they simultaneously grade honesty and information: Each forecaster can be evaluated separately upon their predicted probabilities. The one that is most informed (producing close-to-1 and close-to-0 probabilities) while being honest at the same time will win the quiz. Different scoring rules can then rank strong-but-slightly-uncalibrated against weaker-but-calibrated predictions differently.
As mentioned above, honesty and calibration are not equivalent in practice. We might truly believe 100 times that certain events should occur in 20% of each case — but the true number of occurrences might significantly differ from 20. We might be honest about our belief and express P=Q, but that belief itself is typically uncalibrated! Kahneman and Tversky have studied the cognitive biases that typically make more confident than we should be. In a way, we often behave as if a linear scoring rule judged our predictions, making us lean towards the bold side.