Equations of Motion in the Earth-Moon System | HackerNoon

Table of Links

Abstract and 1. Introduction

2. Clock in Orbit

   2.1 Coordinate Time

   2.2 Local Frame for the Moon

3. Clock Rate Differences Between Earth and Moon

4. Clocks at Earth-Moon Lagrance Points

   4.1 Clock at Lagrange point L1

   4.2. Clock at Lagrange point L2

   4.3. Clock at Lagrange point L4 or L5

5. Conclusions

Appendix 1: Fermi Coordinates with Origin at the Center of the Moon

Appendix 2: Construction of Freely Falling Center of Mass Frame

Appendix 3: Equations of Motion of Earth and Moon

Appendix 4: Comparing Results in Rotating and Non-Rotating Coordinate Systems

Acknowledgments and References

APPENDIX 3: EQUATIONS OF MOTION OF EARTH AND MOO

This partial derivative must be evaluated at the Earth’s center, which would introduce a singularity. However, a body cannot cause the acceleration of its own center of mass so the term involving the Earth’s potential must be “effaced”, or discarded. The equation of motion of the Earth then becomes

A similar argument for the equation of the Moon gives

The center of mass of the Earth-Moon system should be at

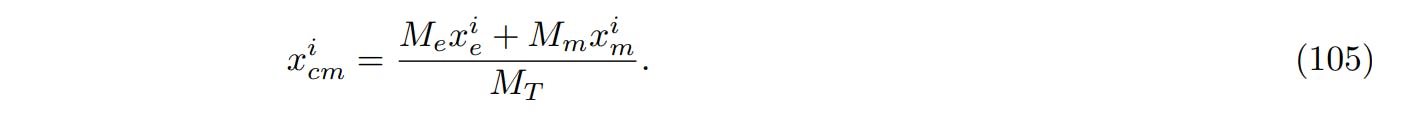
Taking the corresponding linear combinates of the above equations of motion gives

thus verifying that the center of mass of the Earth-Moon system is not accelerated in this coordinate system.

Let the vector from the center of the Earth to the center of the Moon be denoted by D. Then taking the difference between the above two equations of motion gives

where the distance between Earth and the Moon is given by Eq. (19). Then

The Earth-Moon system satisfies Kepler’s equation in the plane of the Earth-Moon orbit:

In summary, we have constructed a locally inertial, freely-falling frame of reference with origin at the center of mass of the Earth and Moon, and have shown that the Earth and Moon revolve about their mutual center of mass in a Keplerian orbit. The coordinates are not normal Fermi coordinates in the sense that the Christoffel symbols of the second kind are not zero at the origin of coordinates when calculated in these coordinates. This is because the geodesic along which the origin falls does not account for forces on a test particle at the origin due to Earth and Moon–only forces due to the Sun are accounted for.